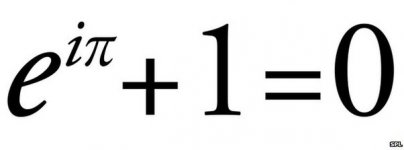Where math meets physics
---
Math and physics are two closely connected fields.
For physicists, math is a tool used to answer questions.
For example, Newton invented calculus to help describe motion.
For mathematicians, physics can be a source of inspiration,
with theoretical concepts such as general relativity and
quantum theory providing an impetus for mathematicians
to develop new tools.
----
But despite their close connections, physics and math research
relies on distinct methods. As the systematic study of how matter
behaves, physics encompasses the study of both the great and
the small, from galaxies and planets to atoms and particles.
Questions are addressed using combinations of theories, experiments,
models, and observations to either support or refute new ideas about
the nature of the universe.
---
In contrast, math is focused on abstract topics such as quantity
(number theory), structure (algebra), and space (geometry).
Mathematicians look for patterns and develop new ideas and
theories using pure logic and mathematical reasoning.
Instead of experiments or observations, mathematicians
use proofs to support their ideas.
---
While physicists rely heavily on math for calculations in their work,
they don’t work towards a fundamental understanding of abstract
mathematical ideas in the way that mathematicians do.
Physicists “want answers, and the way they get answers is by doing
computations,” says mathematician Tony Pantev. “But in mathematics,
the computations are just a decoration on top of the cake.
You have to understand everything completely, then you do a computation.”
----
This fundamental difference leads researchers in both fields to use the analogy
of language, highlighting a need to “translate” ideas in order to make progress
and understand one another. “We are dealing with how to formulate physics
questions so it can be seen as a mathematics problem” says physicist Mirjam Cvetič .
“That’s typically the hardest part.”
----
Kamien works on physics problems in that have a strong connection to geometry
and topology and encourages his students to understand problems as mathematicians do.
“Understanding things for the sake of understanding them is worthwhile, and connecting
them to things that other people know is also worthwhile,” he says.
---
“A physicist comes to us, asks, ‘How do you prove that this is true?’
and we immediately show them it’s false,” says mathematician Ron Donagi.
“But we keep talking, and the trick is not to do what they say to do
but what they mean, a translation of the problem.”
----
Adding extra symmetries makes string theory problems easier to work
with and allows researchers to ask questions about the properties
of geometric structures and how they correspond to real-world physics.
---
Using their physics intuition, Lawrie and Lin were able to apply
their knowledge of math to make new discoveries that wouldn’t
have been possible if the two fields were used in isolation.
“What we found seems to suggest that theories in five dimensions
come from theories in six dimensions,” explains Lin.
“That is something that mathematicians, if they didn’t know
about string theory or physics, would not think about.”
----
Lawrie adds that being able to work directly with mathematicians
is also helpful in their field since understanding new math research
can be a challenge, even for theoretical physics researchers.
“As physicists, we can have a long discussion where we use a lot of intuition,
but if you talk to a mathematician they will say,
‘Wait, precisely what do you mean by that?’ and then you have to pull out
your important assumptions,” says Lawrie. “
It’s also good for clarifying our own thought process.”
---
https://penntoday.upenn.edu/news/where-math-meets-physics
============
---
Math and physics are two closely connected fields.
For physicists, math is a tool used to answer questions.
For example, Newton invented calculus to help describe motion.
For mathematicians, physics can be a source of inspiration,
with theoretical concepts such as general relativity and
quantum theory providing an impetus for mathematicians
to develop new tools.
----
But despite their close connections, physics and math research
relies on distinct methods. As the systematic study of how matter
behaves, physics encompasses the study of both the great and
the small, from galaxies and planets to atoms and particles.
Questions are addressed using combinations of theories, experiments,
models, and observations to either support or refute new ideas about
the nature of the universe.
---
In contrast, math is focused on abstract topics such as quantity
(number theory), structure (algebra), and space (geometry).
Mathematicians look for patterns and develop new ideas and
theories using pure logic and mathematical reasoning.
Instead of experiments or observations, mathematicians
use proofs to support their ideas.
---
While physicists rely heavily on math for calculations in their work,
they don’t work towards a fundamental understanding of abstract
mathematical ideas in the way that mathematicians do.
Physicists “want answers, and the way they get answers is by doing
computations,” says mathematician Tony Pantev. “But in mathematics,
the computations are just a decoration on top of the cake.
You have to understand everything completely, then you do a computation.”
----
This fundamental difference leads researchers in both fields to use the analogy
of language, highlighting a need to “translate” ideas in order to make progress
and understand one another. “We are dealing with how to formulate physics
questions so it can be seen as a mathematics problem” says physicist Mirjam Cvetič .
“That’s typically the hardest part.”
----
Kamien works on physics problems in that have a strong connection to geometry
and topology and encourages his students to understand problems as mathematicians do.
“Understanding things for the sake of understanding them is worthwhile, and connecting
them to things that other people know is also worthwhile,” he says.
---
“A physicist comes to us, asks, ‘How do you prove that this is true?’
and we immediately show them it’s false,” says mathematician Ron Donagi.
“But we keep talking, and the trick is not to do what they say to do
but what they mean, a translation of the problem.”
----
Adding extra symmetries makes string theory problems easier to work
with and allows researchers to ask questions about the properties
of geometric structures and how they correspond to real-world physics.
---
Using their physics intuition, Lawrie and Lin were able to apply
their knowledge of math to make new discoveries that wouldn’t
have been possible if the two fields were used in isolation.
“What we found seems to suggest that theories in five dimensions
come from theories in six dimensions,” explains Lin.
“That is something that mathematicians, if they didn’t know
about string theory or physics, would not think about.”
----
Lawrie adds that being able to work directly with mathematicians
is also helpful in their field since understanding new math research
can be a challenge, even for theoretical physics researchers.
“As physicists, we can have a long discussion where we use a lot of intuition,
but if you talk to a mathematician they will say,
‘Wait, precisely what do you mean by that?’ and then you have to pull out
your important assumptions,” says Lawrie. “
It’s also good for clarifying our own thought process.”
---
https://penntoday.upenn.edu/news/where-math-meets-physics
============